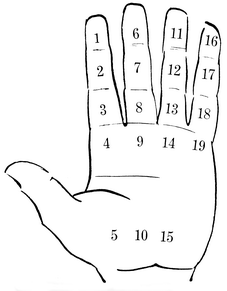
17. mynd. Niðurröðun gyllinitals á höndina
|
III. kafli Að finna páska og aðrar hreyfanlegar kirkjuhátíðir Páskadagur er ævinlega sunnudagur á tímabilinu frá 22. mars til 25. apríl að báðum dögum meðtöldum. Hvaða sunnudagur það er hverju sinni fer eftir ákveðnum reglum sem fylgt hefur verið um langan aldur. Reglur þessar, uppruni þeirra og þróun, eru skýrðar í smáatriðum í grein um grundvöll páskareikningsins. Hér verður aðeins stiklað á því sem máli skiptir í sambandi við fingrarímið. Reglan um páskahald er oftast orðuð á þá leið að páskar skuli vera fyrsta sunnudag eftir fyrstu tunglfyllingu eftir jafndægur á vori. Žessi einfalda regla getur brugšist og gerši žaš reyndar įtta sinnum į 20. öld. Réttara er að orða regluna þannig: Páskadagur skal vera fyrsti sunnudagur eftir fyrsta reiknaðan tunglfyllingardag frá og með 21. mars. Með "reiknaðri" tunglfyllingu er átt við dagsetningu sem áætluð er eftir sérstökum reiknireglum. Raunveruleg tunglfylling er stundum degi fyrr eða síðar eins og útskýrt er í áðurnefndri grein. Þegar talað er um tunglfyllingu hér á eftir er ætíð átt við reiknaða tunglfyllingu fremur en raunverulega, en lesandinn getur látið sér þann greinarmun í léttu rúmi liggja. Að finna tunglfyllinguna, þ. e. fyrstu tunglfyllingu frá
og með 21. mars, er kjarni páskareikningsins. Til þess
eru notaðar tvær hjálpartölur, gyllinital
og paktar. Gyllinital tiltekins árs er tala frá 1
til 19 sem segir til um stöðu ársins í svonefndri
tunglöld, en paktar ársins eru tala frá 0 til 29 (eða
1 til 30) sem í vissum skilningi jafngildir aldri tungls á
nýársdag, þ. e. dagafjöldanum sem þá
er liðinn frá nýju tungli. Í gamla stíl
voru páskareglurnar þannig að tunglfyllingin var ákvörðuð
eftir gyllinitali, en páskareglur nýja stíls kveða
svo á að tunglfyllingin skuli ákvarðast af pöktum.
Af þessu mætti draga þá ályktun að
við ættum ýmist að nota gyllinital eða pakta til
að finna fyllingardag páskatunglsins, allt eftir því
hvort ártalið tilheyrir gamla stíl eða nýja
stíl. Þessu er þó ekki þannig farið
því að gyllinital og paktar eru nátengdar tölur,
sem hægt er að leiða hvora af annarri. Í fingrarími
Jóns biskups Árnasonar er gyllinitalið eitt notað
til þess að finna tunglfyllinguna enda þótt reglurnar
séu samdar fyrir nýja stíl. Hliðstæða
aðferð valdi enska biskupakirkjan síðar í páskareikningi
sínum og notar enn. Er það út af fyrir sig ágæt
leið meðan sambandið milli gyllinitals og pakta helst í
óbreyttri mynd, eins og t. d. á tímabilinu 1700-1899
sem páskareglur Jóns biskups miðast við. En þegar
um lengri tímaskeið er að ræða, verður að
gera lagfæringar sem eru fremur ólánlegar, að minnsta
kosti í fingraríminu. Ég hef því kosið
að innleiða pakta í páskareikning fingrarímsins
og nota paktana til að finna tunglfyllinguna, ekki einasta í
nýja stíl, heldur líka í gamla stíl.
Þótt ótrúlegt megi virðast, eru þessar
nýju fingrarímsreglur auðlærðari en hinar takmarkaðri
reglur í fingrarími Jóns. Í báðum
tilvikum er þó fyrsta skrefið hið sama, að finna
gyllinital ársins, því að paktana er auðveldast
að reikna út frá gyllinitalinu. Skulum við þá
snúa okkur að þessu verkefni.
Gyllinital fundið með fingrarími Á vinstri hendi veljum við 19 staði sem við tileinkum gyllinitölunum frá 1 til 19 (sjá 17. mynd). Staðirnir eru allir á hendinni innanverðri. Gyllinitalið 1 er sett á framlið vísifingurs, 2 á miðlið vísifingurs, 3 á upplið vísifingurs, 4 á rót vísifingurs, 5 á handarrótina upp af vísifingri, 6 á framlið löngutangar, 7 á miðlið löngutangar, 8 á upplið löngutangar o. s. frv. þar til komið er að tölunni 19 sem lendir á rót litlafingurs. |

17. mynd. Niðurröðun gyllinitals á höndina
|
Árið 1900 var fyrsta ár í tunglöld og hefur því gyllinitalið 1. Það ár á því heima á sama stað og gyllinitalið 1, þ. e. fremst á vísifingri. Næsta ár, 1901, hefur gyllinitalið 2 og á því heima á miðlið vísifingurs. Svona getum við haldið áfram og raðað ártölunum á höndina eins og sýnt er á 18. mynd. |
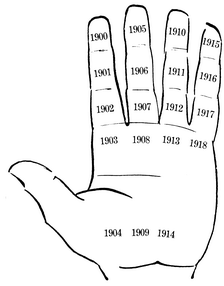
18. mynd. Niðurröðun áranna 1900-1918 eftir gyllinitali
|
Síðasta ár umræddrar tunglaldar var 1918 sem lendir á rót litlafingurs og hefur gyllinitalið 19. |
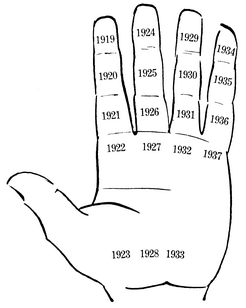
19. mynd. Niðurröðun áranna 1919-1937 eftir gyllinitali
|
Með næsta ári, 1919, hefst ný tunglöld. Það ár er því sett á sama stað og árið 1900, á framlið vísifingurs, og svo koll af kolli þar til komið er að árinu 1937 sem fær síðasta sætið. Á 19. mynd er sýnt hvernig tunglöldin 1919 1937 situr á hendinni. Með hliðsjón af myndinni getum við sem hægast snúið dæminu við og fundið gyllinitöl áranna í þessari tunglöld með því að athuga hvar á hendinni þau sitja. Árið 1930, til dæmis, er á miðlið baugfingurs og hefur því gyllinitalið 12, sbr. 17. mynd. Þriðja tunglöldin eftir 1900 (frá 1938 til 1956)
er sýnd á 20. mynd. Af síðustu þremur myndum
hlýtur að vera ljóst, að við getum rakið
okkur eins langt fram í tímann og þörf krefur
og fundið gyllinitöl allra ára eftir 1900, einfaldlega
með því að athuga hvar á hendinni árin
lenda. Í hvert sinn sem við komum að síðasta
staðnum, rót litlafingurs, er byrjað aftur á fyrsta
stað, framlið vísifingurs. Eina vandamálið er
að þessi aðferð verður of seinleg ef við þurfum
að fara mjög langt fram í tímann. Þá
er nauðsynlegt að geta stytt sér leið.
|
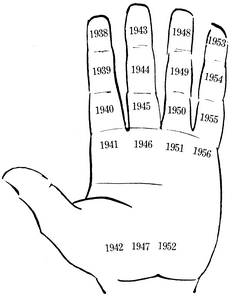
20. mynd. Niðurröðun áranna 1938-1956 eftir gyllinitali
|
Ef við berum saman myndir nr. 18, 19 og 20 og íhugum málið, sjáum við að árin 1900, 1920, 1940, 1960 o. s. frv. hafa gyllinitölin 1, 2, 3, 4 o.s.frv. og mynda því keðju á hendinni (sjá 21. mynd). |
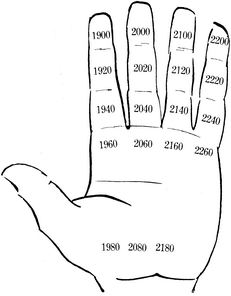
21. mynd. Niðurröðun tuttugasta hvers árs frá 1900 til 2260 eftir gyllinitali
|
Þarna er fundin regla sem er til mikils flýtisauka. Ef við ætlum til dæmis að finna gyllinital ársins 1970 verður aðferðin þessi (sjá 22. mynd). Við byrjum á árinu 1900 sem við munum að situr á framlið vísifingurs. Þaðan stökkvum við til 1920 á miðlið vísifingurs, 1940 á upplið vísifingurs og 1960 á rót vísifingurs. Síðan færum við okkur fram um eitt ár í einu. Árið 1961 verður þá á handarrótinni upp af vísifingri, 1962 á framlið löngutangar, 1963 á miðlið löngutangar, 1964 á upplið löngutangar, 1965 á rót löngutangar, 1966 á handarrótinni upp af löngutöng, 1967 á framlið baugfingurs, 1968 á miðlið baugfingurs, 1969 á upplið baugfingurs og 1970 á rót baugfingurs. Til þess að finna hvaða tala stendur þar, teljum við eins og gert er á 17. mynd, og fæst þá talan 14. Gyllinital ársins 1970 er því 14. |
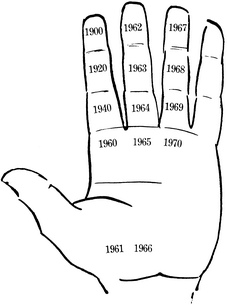
22. mynd. Fundið gyllinital ársins 1970
|
Með hliðsjón af 21. mynd getum við líka rakið okkur aftur í tímann í 20 ára stökkum. Árið 1900 er fremst í keðjunni svo að árið 1880 lendir í hinum enda keðjunnar, þ. e. á rót litlafingurs; 1860 lendir á upplið litlafingurs, 1840 á miðlið litlafingurs, o. s. frv., sjá 23. mynd. Með árinu 1520 erum við aftur komin fremst á vísifingur. Ef við vildum fara enn lengra, myndi árið 1500 falla á sama stað og 1880, o. s. frv. |
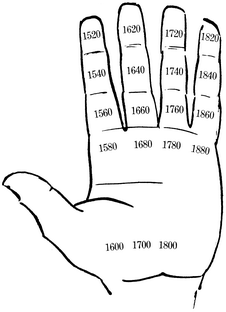
23. mynd. Niðurröðun tuttugasta hvers árs frá 1520 til 1880 eftir gyllinitali
|
En þótt auðvelt sé að rekja sig þannig aftur á bak í 20 ára stökkum, verður það samt full seinlegt ef við þurfum að fara margar aldir aftur í tímann. Þá er betra að leggja sér strax á minni hvar sjálf aldamótaárin sitja á hendinni. Mynd nr. 23 gefur þegar nokkra vísbendingu um þetta, en 24. mynd segir söguna alla. Við sjáum að hvert aldamótaár er 5 sætum framar en næsta aldamótaár á undan svo að aldamótaárin mynda raðir þvert á fingurna. |
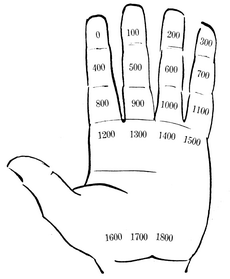
24. mynd. Niðurröðun aldamótaára eftir gyllinitali
|
Eins og annars staðar í þessari grein er talan 0 notuð til að tákna árið 1 f. Kr. (hið næsta á undan árinu 1 e. Kr.), og er þetta gert vegna tölulegs samræmis svo að auðveldara verði að muna reglurnar. Talan 0 situr fremst á vísifingri, 100 fremst á löngutöng, 200 fremst á baugfingri, 300 fremst á litlafingri, 400 á miðlið vísifingurs, o. s. frv. þar til komið er upp í 1800 á handarrótinni upp af löngutöng. Er þá hvert sæti skipað. Með árinu 1900 hefst önnur umferð, og lendir þá 1900 á sama stað og 0, 2000 á sama stað og 100, og svo framvegis, samanber mynd nr. 21. Við skulum nú til dæmis finna gyllinital ársins 1241. Fyrst hlaupum við á aldamótaárunum, byrjum að telja 0 á framlið vísifingurs, 100 á framlið löngutangar, 200 á framlið baugfingurs, 300 á framlið litlafingurs, 400 á miðlið vísifingurs, 500 á miðlið löngutangar, 600 á miðlið baugfingurs, 700 á miðlið litlafingurs, 800 á upplið vísifingurs, 900 á upplið löngutangar, 1000 á upplið baugfingurs, 1100 á upplið litlafingurs og 1200 á rót vísifingurs. Síðan tökum við 20-ára stökk: 1200 á rót vísifingurs, 1220 á handarrótinni upp af vísifingri og 1240 á framlið löngutangar. Þá er 1241 á næsta lið, miðlið löngutangar. Hvaða gyllinital stendur þar? Við teljum frá framlið vísifingurs, samanber 17. mynd, og finnum að á miðlið löngutangar stendur talan 7. Það er þá gyllinital ársins 1241. Aðferðin sem hér hefur verið lýst er grundvölluð
á þeirri sem Jón biskup Árnason notar í
fingrarími sínu. Aðalbreytingin er sú að árið
1900 hefur verið flutt á hentugri stað. Um leið fellur
niður sú viðbótarregla Jóns, að tölunni
10 skuli bætt við allar útkomur.
Reikniregla til að finna gyllinital Gyllinital sérhvers árs eftir Krists burð má finna með þeirri einföldu aðferð að deila í ártalið með 19. Afgangurinn er þá einum lægri en gyllinitalið. Tökum árið 1900 sem dæmi. Þegar deilt er
í 1900 með 19 fæst 0 í afgang. Gyllinital ársins
1900 er þá einum hærra en 0, sem sé 1. Meðfylgjandi
tafla sýnir gyllinitöl allra ára fra 1000 til 2199 e.
Kr.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 24 43 62 81 |
|
|
|
|
|
|
|
|
|
|
|
|
| 6 25 44 63 82 |
|
|
|
|
|
|
|
|
|
|
|
|
| 7 26 45 64 83 |
|
|
|
|
|
|
|
|
|
|
|
|
| 8 27 46 65 84 |
|
|
|
|
|
|
|
|
|
|
|
|
| 9 28 47 66 85 |
|
|
|
|
|
|
|
|
|
|
|
|
| 10 29 48 67 86 |
|
|
|
|
|
|
|
|
|
|
|
|
| 11 30 49 68 87 |
|
|
|
|
|
|
|
|
|
|
|
|
| 12 31 50 69 88 |
|
|
|
|
|
|
|
|
|
|
|
|
| 13 32 51 70 89 |
|
|
|
|
|
|
|
|
|
|
|
|
| 14 33 52 71 90 |
|
|
|
|
|
|
|
|
|
|
|
|
| 15 34 53 72 91 |
|
|
|
|
|
|
|
|
|
|
|
|
| 16 35 54 73 92 |
|
|
|
|
|
|
|
|
|
|
|
|
| 17 36 55 74 93 |
|
|
|
|
|
|
|
|
|
|
|
|
| 18 37 56 75 94 |
|
|
|
|
|
|
|
|
|
|
|
|
| Paktar fundnir með fingrarími
Þegar gyllinital ársins er þekkt, er auðvelt að finna paktana með fingrarími. Við notum nú þumalfingurinn í fyrsta sinn og merkjum á honum þrjá staði (sjá 25. mynd). Á fingurrótina setjum við töluna 0, á uppliðinn töluna 10 og á framliðinn töluna 20 (þumalfingurinn hefur engan miðlið).
25. mynd. Paktar fundnir eftir gyllinitali Tökum nú árið 1970 sem dæmi upp á paktareikning. Við höfðum áður fundið að gyllinital þess árs var 14. Við byrjum nú að telja eftir þumalfingrinum og teljum upp að 14. Fyrst teljum við 1 á rótinni, 2 á upplið og 3 á framlið, síðan 4 aftur á rótinni, 5 á upplið, 6 á framlið, þá 7 á rótinni, 8 á upplið, 9 á framlið, 10 á rótinni, 11 á upplið, 12 á framlið, 13 á rótinni og 14 á upplið. Gyllinitalið 14 lendir sem sagt á upplið þumalfingurs þar sem stendur talan 10. Þetta merkir að við eigum að bæta tölunni 10 við gyllinitalið. Útkoman verður 14+10 = 24. Frá þeirri tölu drögum við nú 2, en sú tala nefnist paktaleiðrétting. Þá fáum við 24–2 = 22, og þar með höfum við fundið pakta ársins 1970. Tökum annað dæmi. Árið 1969 er næsta ár á undan 1970 og hefur því gyllinitalið 13. Við teljum eftir þumalfingrinum á sama hátt og áður, byrjum með 1 á rótinni, 2 á upplið, 3 á framlið o. s. frv., og endum loks með 13 á rótinni. Þar stendur talan 0, sbr. 25. mynd. Við leggjum saman 13+0 = 13. Paktaleiðréttingin er –2 eins og áður. 13–2 = 11, sem eru þá paktar ársins 1969. Tökum þriðja dæmið. Árið 1971 hefur
gyllinitalið 15, einum hærra en gyllinital ársins 1970.
Við teljum á þumalfingrinum og finnum 15 á framlið
þumalfingurs. Þar stendur talan 20. Við leggjum saman 15+20
= 35. Síðan kemur paktaleiðréttingin: 35–2 = 33.
Þá ættu paktarnir að vera 33. En paktatalan getur
ekki orðið hærri en 30; paktarnir 30 jafngilda 0, 31 jafngildir
1, 32 jafngilda 2 o.s.frv. Þess vegna drögum við 30 frá
útkomunni ef hún fer yfir 30. Sem sagt: 33–30 = 3, svo að
paktar ársins 1971 eru 3.
Paktaleiðréttingin Áður en skilist er við paktana verður að fara
nokkrum orðum um paktaleiðréttinguna. Í dæmunum
hér að ofan var notuð paktaleiðréttingin –2 (mínus
tveir). Í nýja stíl var paktaleiðréttingin
0 fram til ársins 1699, síðan –1 fyrir árin 1700-1899,
og nú –2 fyrir árin 1900-2199 að báðum meðtöldum.
Ef við tökum upp sams konar paktareikning til að finna páska
í gamla stíl kemur í ljós að paktaleiðréttingin
þar verður ávallt +7. Nú gekk nýi stíll
í gildi hér á landi seint á árinu 1700.
Við fáum því eftirfarandi töflu fyrir paktaleiðréttingu
til páskareiknings á Íslandi:
Dæmi: Árið 1241 var gyllinitalið 7 eins og áður er sýnt. Við teljum á þumalfingri og finnum að talan 7 lendir á rótinni. Þar stendur talan 0. Við leggjum saman 7+0 = 7. Paktaleiðréttingin er +7, og með því að leggja hana við fáum við 7+7 = 14, sem eru þá paktar ársins 1241. Annað dæmi: Árið 1898 hefur gyllinitalið 18. Við teljum á þumalfingri og finnum að 18 lendir á framliðnum, þar sem talan 20 stendur. 18+20 = 38. Paktaleiðréttingin er –1. 38–1 = 37. Útkoman er yfir 30 svo að við drögum 30 frá; 37–30 = 7. Paktar ársins 1898 eru þá 7. Þriðja dæmi: 1900 hefur gyllinitalið 1. Talan 1
lendir á rót þumalfingurs, þar sem núllið
stendur. 1+0= 1. Paktaleiðréttingin er –2, svo að við
ættum að draga 2 frá 1, en þá yrði útkoman
neikvæð. Þetta getur aðeins gerst þegar gyllinitalið
er 1. Vandinn er auðleystur: á sama hátt og við gátum
dregið 30 frá útkomunni þegar þess gerðist
þörf, getum við lagt 30 við þegar því
er að skipta. 1+30 = 31. Nú getum við dregið 2 frá;
31–2 = 29, og sú tala er paktarnir.
Reikniregla til að finna pakta Ef sett er upp stærðfræðileg reikniregla til að finna pakta, verður hún allflókin. Ég ætla að tilfæra regluna hér, þótt lesandanum sé ekki ætlað að leggja hana á minnið. Takið ártalið og deilið í það með 19. Afganginn skal margfalda með 11, leggja þar við 8, draga frá aldatalið (fyrir 1970 er aldatalið 19), leggja síðan við fjórðung aldatalsins (að afgangi slepptum) og bæta loks við þeirri tölu sem fæst þegar aldatalið er margfaldað með 8, 13 bætt við og deilt í með 25 (afgangi sleppt). Í töluna sem þá kemur út er deilt með 30, og er afgangurinn þá paktarnir. Dæmi: 1970. Við deilum 19 upp í 1970, fáum 13 í afgang, margföldum þá tölu með 11 og fáum 143. Þar við bætast 8, sem gefa 151. Við drögum frá aldatalið 19 og höfum þá eftir 132. Síðan leggst við fjórðungurinn af 19, sem er 4, og fæst þá 136. Loks tökum við 19, margföldum með 8 (= 152), bætum 13 við (= 165) og deilum með 25. Útkoman þar er 6 sem við leggjum nú við 136 og fáum 142. Í þá tölu deilum við með 30. Afgangur verður 22, og eru það paktar ársins. Ofangreind regla gildir fyrir nýja stíl. Fyrir gamla stíl gildir styttri regla: Takið ártalið og deilið í það með 19. Afganginn skal margfalda með 11 og leggja 8 við. Síðan er deilt í útkomuna með 30, og er afgangurinn þá paktarnir. Tafla VII sýnir pakta allra ára frá 1000 til 2199 e. Kr. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 24 43 62 81 |
|
|
|
|
|
|
|
|
|
|
|
|
| 6 25 44 63 82 |
|
|
|
|
|
|
|
|
|
|
|
|
| 7 26 45 64 83 |
|
|
|
|
|
|
|
|
|
|
|
|
| 8 27 46 65 84 |
|
|
|
|
|
|
|
|
|
|
|
|
| 9 28 47 66 85 |
|
|
|
|
|
|
|
|
|
|
|
|
| 10 29 48 67 86 |
|
|
|
|
|
|
|
|
|
|
|
|
| 11 30 49 68 87 |
|
|
|
|
|
|
|
|
|
|
|
|
| 12 31 50 69 88 |
|
|
|
|
|
|
|
|
|
|
|
|
| 13 32 51 70 89 |
|
|
|
|
|
|
|
|
|
|
|
|
| 14 33 52 71 90 |
|
|
|
|
|
|
|
|
|
|
|
|
| 15 34 53 72 91 |
|
|
|
|
|
|
|
|
|
|
|
|
| 16 35 54 73 92 |
|
|
|
|
|
|
|
|
|
|
|
|
| 17 36 55 74 93 |
|
|
|
|
|
|
|
|
|
|
|
|
| 18 37 56 75 94 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Taflan miðast við tímatal á Íslandi, þ.e. gamla stíl fram til 1700 en nýja stíl frá og með 1701. Í efstu línunni, fyrir neðan 1700, gildir fyrri talan (17) aðeins fyrir sjálft aldamótaárið 1700, en síðari talan (9) fyrir önnur ár í sömu línu (1719, 1738, 1757, 1776 og 1795). Paktarnir 25* jafngilda 26 eins og útskýrt er í greininni um grundvöll páskareikningsins. Páskarnir Eftir þetta langa forspjall er nú loksins að því komið að sýna hvernig finna skal sjálfa páskana. Eins og fyrr er sagt getur páskadagur verið einhver daganna 22. mars til 25. apríl að báðum meðtöldum. Þeim 35 dagsetningum sem þarna er um að ræða röðum við nú niður á fingurna og notum til þess fjóra fingur vinstri handar og einn fingur (litlafingur) hægri handar eins og sýnt er á 26. mynd.
26. mynd. Niðurröðun dagsetninga (21. mars til 25. apríl) fyrir páskareikning Við setjum 22. mars á upplið vísifingurs innanverðan, 23. mars á miðlið vísifingurs innanverðan, 24. mars á framlið vísifingurs innanverðan, 25. mars á vísifingurstopp, 26. mars á framlið vísifingurs utanverðan o. s. frv. uns komið er að síðasta deginum, 25. apríl, á utanverðum upplið litlafingurs hægri handar. Dagarnir 1., 8., 15. og 22. apríl lenda á fingurtoppum, og er auðvelt að muna það því að þessi talnaröð kemur oftar fyrir í fingraríminu. Samkvæmt reglunni skal nú páskadagur vera fyrsti sunnudagur eftir fyrsta tunglfyllingardag frá og með 21. mars. Á 26. mynd er 21. mars tekinn með, en þar eð sá dagur hefur sérstöðu að því leyti að hann er ekki hugsanlegur páskadagur, er honum komið fyrir til hliðar, á upplið þumalfingurs. Til þess að geta fundið páskadaginn er nú nauðsynlegt að vita tvennt: hvaða dagur á 26. mynd er tunglfyllingardagur, og hvaða dagar eru sunnudagar. Tökum tunglfyllinguna fyrst. Hana finnum við út frá pöktunum. Við hugsum okkur þá að paktatölunum frá 0 til 29 sé raðað á vinstri höndina eins og sýnt er á 27. mynd. Paktatölurnar ganga ekki í sömu átt og dagsetningamar heldur í öfugan hring eftir fingrunum, en það er reyndar sú leiðin sem venjulegri er í fingraríminu. Byrjað er með 0 á innanverðum miðlið litlafingurs og talið fram á 23 á upplið þumalfingurs. Þaðan er stokkið yfir á utanverðan upplið litlafingurs og hringnum lokað við 30 = 0.
Þarna þarf að koma 30 tölum fyrir á 29 stöðum, og hlýtur því ein talan að ganga af. Til þess er valin talan 25, og er henni að jafnaði komið fyrir á sama stað og tölunni 24. Eftir 1900 (og fram til ársins 2200) er hún hins vegar látin fylgja tölunni 26 og jafnframt auðkennd með stjörnu (25*). Þetta sérkennilega fyrirkomulag er útskýrt í greininni um grundvöll páskareikningsins. Með þeirri niðurröðun talnanna sem sýnd er á 27. mynd segja paktarnir nú til um fyllingardag páskatunglsins því að myndin er hugsuð sem eins konar lykill að 26. mynd. Þegar paktarnir eru til dæmis 23, verður tunglfyllingin 21. mars (berið 27. mynd saman við 26. mynd); þegar paktar eru 12 ber tunglfyllinguna upp á 1. apríl, og þegar paktar eru 0 ber tunglfyllinguna upp á 13. apríl. Á einum stað standast tölurnar á: þegar paktar eru 22 er tunglfylling 22. mars, og er gagnlegt að muna það. Annars er best að leggja sér á minni hvar fyrsta paktatalan (0) situr, til þess að geta talið þaðan og fundið hvar á hendinni aðrar paktatölur eru. Næst skulum við huga að sunnudögunum. Í fyrsta kafla fingrarímsins var sýnt hvemig finna skyldi aðfarardag árs. Það var gert á vísifingri vinstri handar, og voru notaðir til þess fingurstaðirnir sjö, þrír að innanverðu, þrír að utanverðu og fingurtoppurinn. Árið 1970, til dæmis, lenti á upplið innanverðum (hafði miðvikudag fyrir aðfarardag). Slíkt má nú heimfæra umsvifalaust upp á 26. mynd, þannig að árið 1970 verða allir dagar sem sitja á upplið innanverðum, á hvaða fingri sem er, sunnudagar (þumalfingurinn er þó ekki meðtalinn). Dagarnir 22. mars, 29. mars, 5. apríl, 12. apríl og 19. apríl eru því sunnudagar það árið. Árið 1971 situr aftur á móti á upplið utanverðum (hefur fimmtudag fyrir aðfarardag), svo að dagarnir 28. mars, 4. apríl, 11. apríl, 18. apríl og 25. apríl eru sunnudagar. Árið 1972 er hlaupár og hefur því tvo fingurstaði, miðlið utanverðan og framlið utanverðan, sem svara til aðfarardaganna föstudags og laugardags. Hér er það seinni staðurinn sem gildir, því að páskarnir eru alltaf eftir hlaupársdag. Á framlið utanverðum standa dagsetningarnar 26. mars, 2. apríl, 9. apríl, 16. apríl og 23. apríl, svo að þessir dagar eru þá sunnudagar árið 1972. Tökum nú dæmi um páskareikning og finnum páskana 1971. Við byrjum á því að leita uppi paktana, sem eru 3 eins og áður var sagt. Síðan teljum við á vinstri hendi (sbr. 27. mynd) 0 á miðlið litlafingurs innanverðum, 1 á upplið litlafingurs innanverðum, 2 á upplið baugfingurs utanverðum og 3 á miðlið baugfingurs utanverðum. Þar er þá tunglfyllingardagurinn. Næst finnum við sunnudagana. Við notum venjulega aðferð til að finna aðfarardag ársins (sjá I. kafla) og komumst að raun um að hann situr á upplið utanverðum. Sérhver dagur á upplið utanverðum er þá sunnudagur. Nú liggur fyrir að finna næsta sunnudag eftir tunglfyllingardaginn. Tunglfyllingardagurinn er á miðlið baugfingurs utanverðum eins og áður er sagt, og ef við rekjum okkur áfram frá þeim stað, finnum við sunnudag strax á næsta lið, á upplið baugfingurs utanverðum. Þar er þá páskadagurinn 1971. Til þess að finna dagsetninguna notum við okkur þá minnisreglu að 22. mars situr á upplið vísifingurs innanverðum, og teljum þaðan allt fram á upplið baugfingurs utanverðan. Þar verður fyrir okkur dagsetningin 11. apríl, sem er þá dagsetning páskadags árið 1971. Í þessu dæmi hefðum við líka getað flýtt fyrir okkur með því að byrja talninguna við 1. apríl, sem situr á toppi löngutangar, stökkva þaðan yfir á 8. apríl, sem er á toppi baugfingurs, og telja þaðan: 9. apríl á framlið baugfingurs utanverðum, 10. apríl á miðlið baugfingurs utanverðum og 11. apríl á upplið baugfingurs utanverðum. Tökum annað dæmi og finnum páskana 1970. Paktar eru 22 svo að tunglfyllingardagurinn er 22. mars og situr á upplið vísifingurs innanverðum. Aðfarardagur ársins er á upplið innanverðum eins og fyrr er sagt svo að tunglfyllingardagurinn sjálfur er sunnudagur. Páskadagur er næsti sunnudagur á eftir samkvæmt reglunni og situr því á upplið löngutangar innanverðum. Með því að telja frá 22. mars komumst við að raun um að dagsetningin er 29. mars. Sem þriðja dæmi skulum við taka páskana 1973. Þar sem ekki var búið að finna pakta þess árs verður að byrja á því. Gyllinitalið er 17, svo að paktarnir verða 17+10–2 = 25. Hér er um að ræða hina sérstöku paktatölu 25* sem áður var getið um, því að á yfirstandandi tímabili (1900-2199) eru paktarnir 25 látnir jafngilda pöktunum 26 og sitja á sama stað á hendinni, sem sé á miðlið litlafingurs utanverðum, sjá 27. mynd. Þar er þá tunglfyllingardagurinn. Næst finnum við aðfarardag ársins á venjulegan hátt, og situr hann á fingurtoppi. Sunnudagarnir eru þá á fingurtoppunum. Næsti fingurtoppur við miðlið litlafingurs utanverðan er toppur litlafingurs hægri handar. Samkvæmt því koma páskarnir 1973 hinn 22. apríl. Verða það sumarpáskar, því að sumardagurinn fyrsti það ár er 19. apríl. Á það má benda, að þær dagsetningar
sem sumardagurinn fyrsti getur fallið á, standa allar á
litlafingri hægri handar (26. mynd). Nú er sumardagurinn fyrsti
ætíð fimmtudagur, svo að sumarpáskar geta í
fyrsta lagi orðið 22. apríl. Með öðrum orðum,
sumarpáskar eru ávallt þegar páskadag ber upp
á einhvern dagana 22.- 25. apríl. Falla þá saman
tveir almennir frídagar, skírdagur og sumardagurinn fyrsti.
Þetta gerist 6 sinnum á hverjum 95 árum, eða að
meðaltali einu sinni á hverjum 16 árum.
Hátíðir sem fylgja páskunum Ýmsir merkisdagar kirkjunnar flytjast til í árinu með páskunum svo sem kunnugt er. Þessa daga er hægt að finna með sömu aðferð og notuð er til að finna páskana, nema hvað dagsetningarnar á fingrunum verða aðrar en þær sem sýndar eru á 26. mynd. Ef við tökum hvítasunnuna sem dæmi, getur hún í fyrsta lagi orðið 10. maí (þegar páskar eru 22. mars). Til þess að finna hvítasunnuna tiltekið ár byrjum við á því að leita uppi fingurstað páskadagsins, en þegar að því kemur að finna þá dagsetningu sem svarar til fingurstaðarins, verðum við í stað 22. mars að setja 10. maí á upplið vísifingurs innanverðan og telja þaðan. Kemur þá 11. maí á miðlið vísifingurs innanverðan, 12. maí á framlið vísifingurs innanverðan o. s. frv. þar til komið er að 13. júní á utanverðum upplið litlafingurs hægri handar, en það er síðasti fingurstaðurinn. Kemur það heim, að hvítasunnan er 13. júní þau ár sem páskana ber upp á 25. apríl. Öskudagur, hvítasunnudagur og uppstigningardagur fylgja
páskunum sem sér segir:
Með því að athuga almanakið getur lesandinn
hæglega fundið fleiri tímamörk, s. s. fyrir níuviknaföstu,
bolludag, sprengidag, pálmasunnudag, kóngsbænadag,
trínitatis og dýradag.
Reiknireglur til að finna páska Þótt fingrarímsreglurnar séu nokkuð fyrirferðarmiklar á prenti, er tiltölulega fljótlegt að ná tökum á þeim. Með nokkurri æfingu ætti lesandinn hæglega að geta fundið páska fyrir hvaða ár sem vera skal á einni mínútu eða svo, og eftir að leikni er náð ætti hálf mínúta að nægja. Slíkum hraða verður seint náð með öðrum aðferðum, nema tölvum sé beitt. Unnt er að setja reglur fingrarímsins fram á stærðfræðilegan hátt og leysa dæmin þannig, en í þeirri framsetningu eru reglurnar fremur flóknar og völ á öðrum betri. Einfaldasta reiknireglan sem ég hef rekist á til að finna páska í gamla stíl er sem hér segir: Deilið í ártalið
með 19 og kallið afganginn a.
Þá er f mánuðurinn sem páskarnir falla í, og g + 1 er mánaðardagurinn. Dæmi: 1700 (síðustu páskar í gamla stíl hér á landi). 1700 deilt með 19 gefur 9 í afgang. Þá er a = 9. 1700 deilt með 7 gefur 6 í afgang. Þá er b = 6. 1700 deilt með 4 gefur 0 í afgang. Þá er c = 0. Við margföldum a (þ. e. 9) með 11 og leggjum 14 við. Útkoman er 113. Þegar deilt er í 113 með 30 verða 23 í afgang. Þá er d = 23. Við leggjum saman tölurnar d (þ. e. 23), 4b (þ. e. 4 * 6 = 24), 2c (þ. e. 2 * 0 = 0) og 5 og fáum út 52. Þegar deilt er í 52 með 7 verða 3 í afgang. Þá er e = 3. Loks tökum við 143, drögum þar frá d (þ. e. 23), leggjum við e (þ. e. 3). Summan verður 123. Við deilum í þá tölu með 31 og fáum 3 í deild og 30 í afgang. Þá er f = 3 og g = 30. Páskana árið 1700 ber því upp á mánuðinn 3 (mars) og daginn 30 + 1 = 31, sem sagt 31. mars. Ofangreind regla er (með örlítilli breytingu) fengin úr franska almanakinu Annuaire du Bureau des Longitudes árið 1968, bls. 411. Um frumheimildina veit ég ekki. Besta reiknireglan til að finna páska í nýja stíl mun vera sú sem birtist nafnlaust í breska tímaritinu Nature árið 1876. Reglan er þessi: Deilið í ártalið
með 19 og kallið afganginn a.
Þá er n mánuðurinn sem páskadagur fellur í, og p + 1 er mánaðardagurinn. Ef við tökum 1971 sem dæmi fáum við a = 14, b = 19, c = 71, d = 4, e = 3, f = 1, g = 6, h = 20, i = 17, j = 3, k = 0, m = 0, n = 4, p = 10. Þá eru páskarnir í 4. mánuði ársins og dagurinn er 10 + 1, þ. e. 11. apríl. Töflurnar hér á eftir sýna páska á
Íslandi frá árinu 1000 til 2199. Kannað var hve
oft hver dagsetning kæmi fyrir á þessu tímabili.
Niðurstaðan varð sem hér segir:
Fyrstu og síðustu dagsetningarnar eru greinilega sjaldgæfari en hinar. Er það að vonum, því að tiltölulega fá paktagildi geta gefið þessar dagsetningar. Til dæmis geta páskar ekki orðið 22. mars nema paktar séu 23, og ekki 25. apríl nema paktar séu 24 eða 25. Á tímabilinu 1900- 2199 ber páskana aldrei upp á 22. mars (paktarnir geta ekki fengið gildið 23). Algengasta dagsetningin á þessu tímabili er 31. mars. Þegar til lengri tíma er horft, hefur 19. apríl þó vinninginn. Kemur það fram í grein um tíðni páskadagsetninga í Almanaki Þjóðvinafélagsins 1983. Í gamla stíl endurtaka dagsetningarnar sig reglubundið á 532 ára fresti (páskaöld). Þannig eru páskarnir árið 1000 sama dag og árið 1532, páskarnir 1001 sama dag og 1533, o. s. frv. Í nýja stíl er samsvarandi tímabil 5 700 000 ár, þannig að tæplega er unnt að segja að um endurtekningu sé að ræða. Í sambandi við páskatöflurnar hér á eftir er rétt að geta þess að hinn stjörnufræðilegi páskareikningur mótmælenda í Þýskalandi á árunum 1700-1776 leiddi tvívegis til þess að páskarnir voru haldnir þar í landi á öðrum degi en vera bar samkvæmt hinum kaþólsku reglum nýja stíls. Var það árin 1724 og 1744. Danakonungur ætlaði að fylgja dæmi þýskra mótmælenda, en varð of seinn í fyrra skiptið, þar sem almanakið fyrir 1724 hafði þegar verið prentað. Í seinna skiptið náði ætlunin fram að ganga, og var páskadagurinn í danska almanakinu 1744 settur við 29. mars en ekki 5. apríl. Að vísu gaf Kaupmannahafnarháskóli út annað almanak sama ár þar sem páskadagur var settur 5. apríl, en það almanak var dæmt ógilt. Hvort einhverjir Íslendingar hafi miðað við hinn afbrigðilega páskadag 29. mars árið 1744 skal ekkert fullyrt um, en slíkt virðist harla ólíklegt. Fingrarím Jóns biskups var þá nýkomið út, og þar er árið 1744 einmitt tekið sem dæmi um páskareikning. Sú dagsetning sem Jón gefur er að sjálfsögðu 5. apríl, enda reglurnar í fullu samræmi við páskareikning nýja stíls. |
| 1000 MAR 31 | 1100 APR 1 | 1200 APR 9 | 1300 APR 10 | 1400 APR 18 | 1500 APR 19 |
| 1001 APR 13 | 1101 APR 21 | 1201 MAR 25 | 1301 APR 2 | 1401 APR 3 | 1501 APR 11 |
| 1002 APR 5 | 1102 APR 6 | 1202 APR 14 | 1302 APR 22 | 1402 MAR 26 | 1502 MAR 27 |
| 1003 MAR 28 | 1103 MAR 29 | 1203 APR 6 | 1303 APR 7 | 1403 APR 15 | 1503 APR 16 |
| 1004 APR 16 | 1104 APR 17 | 1204 APR 25 | 1304 MAR 29 | 1404 MAR 30 | 1504 APR 7 |
| 1005 APR 1 | 1105 APR 9 | 1205 APR 10 | 1305 APR 18 | 1405 APR 19 | 1505 MAR 23 |
| 1006 APR 21 | 1106 MAR 25 | 1206 APR 2 | 1306 APR 3 | 1406 APR 11 | 1506 APR 12 |
| 1007 APR 6 | 1107 APR 14 | 1207 APR 22 | 1307 MAR 26 | 1407 MAR 27 | 1507 APR 4 |
| 1008 MAR 28 | 1108 APR 5 | 1208 APR 6 | 1308 APR 14 | 1408 APR 15 | 1508 APR 23 |
| 1009 APR 17 | 1109 APR 25 | 1209 MAR 29 | 1309 MAR 30 | 1409 APR 7 | 1509 APR 8 |
| 1010 APR 9 | 1110 APR 10 | 1210 APR 18 | 1310 APR 19 | 1410 MAR 23 | 1510 MAR 31 |
| 1011 MAR 25 | 1111 APR 2 | 1211 APR 3 | 1311 APR 11 | 1411 APR 12 | 1511 APR 20 |
| 1012 APR 13 | 1112 APR 21 | 1212 MAR 25 | 1312 MAR 26 | 1412 APR 3 | 1512 APR 11 |
| 1013 APR 5 | 1113 APR 6 | 1213 APR 14 | 1313 APR 15 | 1413 APR 23 | 1513 MAR 27 |
| 1014 APR 25 | 1114 MAR 29 | 1214 MAR 30 | 1314 APR 7 | 1414 APR 8 | 1514 APR 16 |
| 1015 APR 10 | 1115 APR 18 | 1215 APR 19 | 1315 MAR 23 | 1415 MAR 31 | 1515 APR 8 |
| 1016 APR 1 | 1116 APR 2 | 1216 APR 10 | 1316 APR 11 | 1416 APR 19 | 1516 MAR 23 |
| 1017 APR 21 | 1117 MAR 25 | 1217 MAR 26 | 1317 APR 3 | 1417 APR 11 | 1517 APR 12 |
| 1018 APR 6 | 1118 APR 14 | 1218 APR 15 | 1318 APR 23 | 1418 MAR 27 | 1518 APR 4 |
| 1019 MAR 29 | 1119 MAR 30 | 1219 APR 7 | 1319 APR 8 | 1419 APR 16 | 1519 APR 24 |
| 1020 APR 17 | 1120 APR 18 | 1220 MAR 29 | 1320 MAR 30 | 1420 APR 7 | 1520 APR 8 |
| 1021 APR 2 | 1121 APR 10 | 1221 APR 11 | 1321 APR 19 | 1421 MAR 23 | 1521 MAR 31 |
| 1022 MAR 25 | 1122 MAR 26 | 1222 APR 3 | 1322 APR 11 | 1422 APR 12 | 1522 APR 20 |
| 1023 APR 14 | 1123 APR 15 | 1223 APR 23 | 1323 MAR 27 | 1423 APR 4 | 1523 APR 5 |
| 1024 APR 5 | 1124 APR 6 | 1224 APR 14 | 1324 APR 15 | 1424 APR 23 | 1524 MAR 27 |
| 1025 APR 18 | 1125 MAR 29 | 1225 MAR 30 | 1325 APR 7 | 1425 APR 8 | 1525 APR 16 |
| 1026 APR 10 | 1126 APR 11 | 1226 APR 19 | 1326 MAR 23 | 1426 MAR 31 | 1526 APR 1 |
| 1027 MAR 26 | 1127 APR 3 | 1227 APR 11 | 1327 APR 12 | 1427 APR 20 | 1527 APR 21 |
| 1028 APR 14 | 1128 APR 22 | 1228 MAR 26 | 1328 APR 3 | 1428 APR 4 | 1528 APR 12 |
| 1029 APR 6 | 1129 APR 14 | 1229 APR 15 | 1329 APR 23 | 1429 MAR 27 | 1529 MAR 28 |
| 1030 MAR 29 | 1130 MAR 30 | 1230 APR 7 | 1330 APR 8 | 1430 APR 16 | 1530 APR 17 |
| 1031 APR 11 | 1131 APR 19 | 1231 MAR 23 | 1331 MAR 31 | 1431 APR 1 | 1531 APR 9 |
| 1032 APR 2 | 1132 APR 10 | 1232 APR 11 | 1332 APR 19 | 1432 APR 20 | 1532 MAR 31 |
| 1033 APR 22 | 1133 MAR 26 | 1233 APR 3 | 1333 APR 4 | 1433 APR 12 | 1533 APR 13 |
| 1034 APR 14 | 1134 APR 15 | 1234 APR 23 | 1334 MAR 27 | 1434 MAR 28 | 1534 APR 5 |
| 1035 MAR 30 | 1135 APR 7 | 1235 APR 8 | 1335 APR 16 | 1435 APR 17 | 1535 MAR 28 |
| 1036 APR 18 | 1136 MAR 22 | 1236 MAR 30 | 1336 MAR 31 | 1436 APR 8 | 1536 APR 16 |
| 1037 APR 10 | 1137 APR 11 | 1237 APR 19 | 1337 APR 20 | 1437 MAR 31 | 1537 APR 1 |
| 1038 MAR 26 | 1138 APR 3 | 1238 APR 4 | 1338 APR 12 | 1438 APR 13 | 1538 APR 21 |
| 1039 APR 15 | 1139 APR 23 | 1239 MAR 27 | 1339 MAR 28 | 1439 APR 5 | 1539 APR 6 |
| 1040 APR 6 | 1140 APR 7 | 1240 APR 15 | 1340 APR 16 | 1440 MAR 27 | 1540 MAR 28 |
| 1041 MAR 22 | 1141 MAR 30 | 1241 MAR 31 | 1341 APR 8 | 1441 APR 16 | 1541 APR 17 |
| 1042 APR 11 | 1142 APR 19 | 1242 APR 20 | 1342 MAR 31 | 1442 APR 1 | 1542 APR 9 |
| 1043 APR 3 | 1143 APR 4 | 1243 APR 12 | 1343 APR 13 | 1443 APR 21 | 1543 MAR 25 |
| 1044 APR 22 | 1144 MAR 26 | 1244 APR 3 | 1344 APR 4 | 1444 APR 12 | 1544 APR 13 |
| 1045 APR 7 | 1145 APR 15 | 1245 APR 16 | 1345 MAR 27 | 1445 MAR 28 | 1545 APR 5 |
| 1046 MAR 30 | 1146 MAR 31 | 1246 APR 8 | 1346 APR 16 | 1446 APR 17 | 1546 APR 25 |
| 1047 APR 19 | 1147 APR 20 | 1247 MAR 31 | 1347 APR 1 | 1447 APR 9 | 1547 APR 10 |
| 1048 APR 3 | 1148 APR 11 | 1248 APR 19 | 1348 APR 20 | 1448 MAR 24 | 1548 APR 1 |
| 1049 MAR 26 | 1149 APR 3 | 1249 APR 4 | 1349 APR 12 | 1449 APR 13 | 1549 APR 21 |
| 1050 APR 15 | 1150 APR 16 | 1250 MAR 27 | 1350 MAR 28 | 1450 APR 5 | 1550 APR 6 |
| 1051 MAR 31 | 1151 APR 8 | 1251 APR 16 | 1351 APR 17 | 1451 APR 25 | 1551 MAR 29 |
| 1052 APR 19 | 1152 MAR 30 | 1252 MAR 31 | 1352 APR 8 | 1452 APR 9 | 1552 APR 17 |
| 1053 APR 11 | 1153 APR 19 | 1253 APR 20 | 1353 MAR 24 | 1453 APR 1 | 1553 APR 2 |
| 1054 APR 3 | 1154 APR 4 | 1254 APR 12 | 1354 APR 13 | 1454 APR 21 | 1554 MAR 25 |
| 1055 APR 16 | 1155 MAR 27 | 1255 MAR 28 | 1355 APR 5 | 1455 APR 6 | 1555 APR 14 |
| 1056 APR 7 | 1156 APR 15 | 1256 APR 16 | 1356 APR 24 | 1456 MAR 28 | 1556 APR 5 |
| 1057 MAR 30 | 1157 MAR 31 | 1257 APR 8 | 1357 APR 9 | 1457 APR 17 | 1557 APR 18 |
| 1058 APR 19 | 1158 APR 20 | 1258 MAR 24 | 1358 APR 1 | 1458 APR 2 | 1558 APR 10 |
| 1059 APR 4 | 1159 APR 12 | 1259 APR 13 | 1359 APR 21 | 1459 MAR 25 | 1559 MAR 26 |
| 1060 MAR 26 | 1160 MAR 27 | 1260 APR 4 | 1360 APR 5 | 1460 APR 13 | 1560 APR 14 |
| 1061 APR 15 | 1161 APR 16 | 1261 APR 24 | 1361 MAR 28 | 1461 APR 5 | 1561 APR 6 |
| 1062 MAR 31 | 1162 APR 8 | 1262 APR 9 | 1362 APR 17 | 1462 APR 18 | 1562 MAR 29 |
| 1063 APR 20 | 1163 MAR 24 | 1263 APR 1 | 1363 APR 2 | 1463 APR 10 | 1563 APR 11 |
| 1064 APR 11 | 1164 APR 12 | 1264 APR 20 | 1364 MAR 24 | 1464 APR 1 | 1564 APR 2 |
| 1065 MAR 27 | 1165 APR 4 | 1265 APR 5 | 1365 APR 13 | 1465 APR 14 | 1565 APR 22 |
| 1066 APR 16 | 1166 APR 24 | 1266 MAR 28 | 1366 APR 5 | 1466 APR 6 | 1566 APR 14 |
| 1067 APR 8 | 1167 APR 9 | 1267 APR 17 | 1367 APR 18 | 1467 MAR 29 | 1567 MAR 30 |
| 1068 MAR 23 | 1168 MAR 31 | 1268 APR 8 | 1368 APR 9 | 1468 APR 17 | 1568 APR 18 |
| 1069 APR 12 | 1169 APR 20 | 1269 MAR 24 | 1369 APR 1 | 1469 APR 2 | 1569 APR 10 |
| 1070 APR 4 | 1170 APR 5 | 1270 APR 13 | 1370 APR 14 | 1470 APR 22 | 1570 MAR 26 |
| 1071 APR 24 | 1171 MAR 28 | 1271 APR 5 | 1371 APR 6 | 1471 APR 14 | 1571 APR 15 |
| 1072 APR 8 | 1172 APR 16 | 1272 APR 24 | 1372 MAR 28 | 1472 MAR 29 | 1572 APR 6 |
| 1073 MAR 31 | 1173 APR 8 | 1273 APR 9 | 1373 APR 17 | 1473 APR 18 | 1573 MAR 22 |
| 1074 APR 20 | 1174 MAR 24 | 1274 APR 1 | 1374 APR 2 | 1474 APR 10 | 1574 APR 11 |
| 1075 APR 5 | 1175 APR 13 | 1275 APR 14 | 1375 APR 22 | 1475 MAR 26 | 1575 APR 3 |
| 1076 MAR 27 | 1176 APR 4 | 1276 APR 5 | 1376 APR 13 | 1476 APR 14 | 1576 APR 22 |
| 1077 APR 16 | 1177 APR 24 | 1277 MAR 28 | 1377 MAR 29 | 1477 APR 6 | 1577 APR 7 |
| 1078 APR 8 | 1178 APR 9 | 1278 APR 17 | 1378 APR 18 | 1478 MAR 22 | 1578 MAR 30 |
| 1079 MAR 24 | 1179 APR 1 | 1279 APR 2 | 1379 APR 10 | 1479 APR 11 | 1579 APR 19 |
| 1080 APR 12 | 1180 APR 20 | 1280 APR 21 | 1380 MAR 25 | 1480 APR 2 | 1580 APR 3 |
| 1081 APR 4 | 1181 APR 5 | 1281 APR 13 | 1381 APR 14 | 1481 APR 22 | 1581 MAR 26 |
| 1082 APR 24 | 1182 MAR 28 | 1282 MAR 29 | 1382 APR 6 | 1482 APR 7 | 1582 APR 15 |
| 1083 APR 9 | 1183 APR 17 | 1283 APR 18 | 1383 MAR 22 | 1483 MAR 30 | 1583 MAR 31 |
| 1084 MAR 31 | 1184 APR 1 | 1284 APR 9 | 1384 APR 10 | 1484 APR 18 | 1584 APR 19 |
| 1085 APR 20 | 1185 APR 21 | 1285 MAR 25 | 1385 APR 2 | 1485 APR 3 | 1585 APR 11 |
| 1086 APR 5 | 1186 APR 13 | 1286 APR 14 | 1386 APR 22 | 1486 MAR 26 | 1586 APR 3 |
| 1087 MAR 28 | 1187 MAR 29 | 1287 APR 6 | 1387 APR 7 | 1487 APR 15 | 1587 APR 16 |
| 1088 APR 16 | 1188 APR 17 | 1288 MAR 28 | 1388 MAR 29 | 1488 APR 6 | 1588 APR 7 |
| 1089 APR 1 | 1189 APR 9 | 1289 APR 10 | 1389 APR 18 | 1489 APR 19 | 1589 MAR 30 |
| 1090 APR 21 | 1190 MAR 25 | 1290 APR 2 | 1390 APR 3 | 1490 APR 11 | 1590 APR 19 |
| 1091 APR 13 | 1191 APR 14 | 1291 APR 22 | 1391 MAR 26 | 1491 APR 3 | 1591 APR 4 |
| 1092 MAR 28 | 1192 APR 5 | 1292 APR 6 | 1392 APR 14 | 1492 APR 22 | 1592 MAR 26 |
| 1093 APR 17 | 1193 MAR 28 | 1293 MAR 29 | 1393 APR 6 | 1493 APR 7 | 1593 APR 15 |
| 1094 APR 9 | 1194 APR 10 | 1294 APR 18 | 1394 APR 19 | 1494 MAR 30 | 1594 MAR 31 |
| 1095 MAR 25 | 1195 APR 2 | 1295 APR 3 | 1395 APR 11 | 1495 APR 19 | 1595 APR 20 |
| 1096 APR 13 | 1196 APR 21 | 1296 MAR 25 | 1396 APR 2 | 1496 APR 3 | 1596 APR 11 |
| 1097 APR 5 | 1197 APR 6 | 1297 APR 14 | 1397 APR 22 | 1497 MAR 26 | 1597 MAR 27 |
| 1098 MAR 28 | 1198 MAR 29 | 1298 APR 6 | 1398 APR 7 | 1498 APR 15 | 1598 APR 16 |
| 1099 APR 10 | 1199 APR 18 | 1299 APR 19 | 1399 MAR 30 | 1499 MAR 31 | 1599 APR 8 |
| 1600 MAR 23 | 1700 MAR 31 | 1800 APR 13 | 1900 APR 15 | 2000 APR 23 | 2100 MAR 28 |
| 1601 APR 12 | 1701 MAR 27 | 1801 APR 5 | 1901 APR 7 | 2001 APR 15 | 2101 APR 17 |
| 1602 APR 4 | 1702 APR 16 | 1802 APR 18 | 1902 MAR 30 | 2002 MAR 31 | 2102 APR 9 |
| 1603 APR 24 | 1703 APR 8 | 1803 APR 10 | 1903 APR 12 | 2003 APR 20 | 2103 MAR 25 |
| 1604 APR 8 | 1704 MAR 23 | 1804 APR 1 | 1904 APR 3 | 2004 APR 11 | 2104 APR 13 |
| 1605 MAR 31 | 1705 APR 12 | 1805 APR 14 | 1905 APR 23 | 2005 MAR 27 | 2105 APR 5 |
| 1606 APR 20 | 1706 APR 4 | 1806 APR 6 | 1906 APR 15 | 2006 APR 16 | 2106 APR 18 |
| 1607 APR 5 | 1707 APR 24 | 1807 MAR 29 | 1907 MAR 31 | 2007 APR 8 | 2107 APR 10 |
| 1608 MAR 27 | 1708 APR 8 | 1808 APR 17 | 1908 APR 19 | 2008 MAR 23 | 2108 APR 1 |
| 1609 APR 16 | 1709 MAR 31 | 1809 APR 2 | 1909 APR 11 | 2009 APR 12 | 2109 APR 21 |
| 1610 APR 8 | 1710 APR 20 | 1810 APR 22 | 1910 MAR 27 | 2010 APR 4 | 2110 APR 6 |
| 1611 MAR 24 | 1711 APR 5 | 1811 APR 14 | 1911 APR 16 | 2011 APR 24 | 2111 MAR 29 |
| 1612 APR 12 | 1712 MAR 27 | 1812 MAR 29 | 1912 APR 7 | 2012 APR 8 | 2112 APR 17 |
| 1613 APR 4 | 1713 APR 16 | 1813 APR 18 | 1913 MAR 23 | 2013 MAR 31 | 2113 APR 2 |
| 1614 APR 24 | 1714 APR 1 | 1814 APR 10 | 1914 APR 12 | 2014 APR 20 | 2114 APR 22 |
| 1615 APR 9 | 1715 APR 21 | 1815 MAR 26 | 1915 APR 4 | 2015 APR 5 | 2115 APR 14 |
| 1616 MAR 31 | 1716 APR 12 | 1816 APR 14 | 1916 APR 23 | 2016 MAR 27 | 2116 MAR 29 |
| 1617 APR 20 | 1717 MAR 28 | 1817 APR 6 | 1917 APR 8 | 2017 APR 16 | 2117 APR 18 |
| 1618 APR 5 | 1718 APR 17 | 1818 MAR 22 | 1918 MAR 31 | 2018 APR 1 | 2118 APR 10 |
| 1619 MAR 28 | 1719 APR 9 | 1819 APR 11 | 1919 APR 20 | 2019 APR 21 | 2119 MAR 26 |
| 1620 APR 16 | 1720 MAR 31 | 1820 APR 2 | 1920 APR 4 | 2020 APR 12 | 2120 APR 14 |
| 1621 APR 1 | 1721 APR 13 | 1821 APR 22 | 1921 MAR 27 | 2021 APR 4 | 2121 APR 6 |
| 1622 APR 21 | 1722 APR 5 | 1822 APR 7 | 1922 APR 16 | 2022 APR 17 | 2122 MAR 29 |
| 1623 APR 13 | 1723 MAR 28 | 1823 MAR 30 | 1923 APR 1 | 2023 APR 9 | 2123 APR 11 |
| 1624 MAR 28 | 1724 APR 16 | 1824 APR 18 | 1924 APR 20 | 2024 MAR 31 | 2124 APR 2 |
| 1625 APR 17 | 1725 APR 1 | 1825 APR 3 | 1925 APR 12 | 2025 APR 20 | 2125 APR 22 |
| 1626 APR 9 | 1726 APR 21 | 1826 MAR 26 | 1926 APR 4 | 2026 APR 5 | 2126 APR 14 |
| 1627 MAR 25 | 1727 APR 13 | 1827 APR 15 | 1927 APR 17 | 2027 MAR 28 | 2127 MAR 30 |
| 1628 APR 13 | 1728 MAR 28 | 1828 APR 6 | 1928 APR 8 | 2028 APR 16 | 2128 APR 18 |
| 1629 APR 5 | 1729 APR 17 | 1829 APR 19 | 1929 MAR 31 | 2029 APR 1 | 2129 APR 10 |
| 1630 MAR 28 | 1730 APR 9 | 1830 APR 11 | 1930 APR 20 | 2030 APR 21 | 2130 MAR 26 |
| 1631 APR 10 | 1731 MAR 25 | 1831 APR 3 | 1931 APR 5 | 2031 APR 13 | 2131 APR 15 |
| 1632 APR 1 | 1732 APR 13 | 1832 APR 22 | 1932 MAR 27 | 2032 MAR 28 | 2132 APR 6 |
| 1633 APR 21 | 1733 APR 5 | 1833 APR 7 | 1933 APR 16 | 2033 APR 17 | 2133 APR 19 |
| 1634 APR 6 | 1734 APR 25 | 1834 MAR 30 | 1934 APR 1 | 2034 APR 9 | 2134 APR 11 |
| 1635 MAR 29 | 1735 APR 10 | 1835 APR 19 | 1935 APR 21 | 2035 MAR 25 | 2135 APR 3 |
| 1636 APR 17 | 1736 APR 1 | 1836 APR 3 | 1936 APR 12 | 2036 APR 13 | 2136 APR 22 |
| 1637 APR 9 | 1737 APR 21 | 1837 MAR 26 | 1937 MAR 28 | 2037 APR 5 | 2137 APR 7 |
| 1638 MAR 25 | 1738 APR 6 | 1838 APR 15 | 1938 APR 17 | 2038 APR 25 | 2138 MAR 30 |
| 1639 APR 14 | 1739 MAR 29 | 1839 MAR 31 | 1939 APR 9 | 2039 APR 10 | 2139 APR 19 |
| 1640 APR 5 | 1740 APR 17 | 1840 APR 19 | 1940 MAR 24 | 2040 APR 1 | 2140 APR 3 |
| 1641 APR 25 | 1741 APR 2 | 1841 APR 11 | 1941 APR 13 | 2041 APR 21 | 2141 MAR 26 |
| 1642 APR 10 | 1742 MAR 25 | 1842 MAR 27 | 1942 APR 5 | 2042 APR 6 | 2142 APR 15 |
| 1643 APR 2 | 1743 APR 14 | 1843 APR 16 | 1943 APR 25 | 2043 MAR 29 | 2143 MAR 31 |
| 1644 APR 21 | 1744 APR 5 | 1844 APR 7 | 1944 APR 9 | 2044 APR 17 | 2144 APR 19 |
| 1645 APR 6 | 1745 APR 18 | 1845 MAR 23 | 1945 APR 1 | 2045 APR 9 | 2145 APR 11 |
| 1646 MAR 29 | 1746 APR 10 | 1846 APR 12 | 1946 APR 21 | 2046 MAR 25 | 2146 APR 3 |
| 1647 APR 18 | 1747 APR 2 | 1847 APR 4 | 1947 APR 6 | 2047 APR 14 | 2147 APR 16 |
| 1648 APR 2 | 1748 APR 14 | 1848 APR 23 | 1948 MAR 28 | 2048 APR 5 | 2148 APR 7 |
| 1649 MAR 25 | 1749 APR 6 | 1849 APR 8 | 1949 APR 17 | 2049 APR 18 | 2149 MAR 30 |
| 1650 APR 14 | 1750 MAR 29 | 1850 MAR 31 | 1950 APR 9 | 2050 APR 10 | 2150 APR 12 |
| 1651 MAR 30 | 1751 APR 11 | 1851 APR 20 | 1951 MAR 25 | 2051 APR 2 | 2151 APR 4 |
| 1652 APR 18 | 1752 APR 2 | 1852 APR 11 | 1952 APR 13 | 2052 APR 21 | 2152 APR 23 |
| 1653 APR 10 | 1753 APR 22 | 1853 MAR 27 | 1953 APR 5 | 2053 APR 6 | 2153 APR 15 |
| 1654 MAR 26 | 1754 APR 14 | 1854 APR 16 | 1954 APR 18 | 2054 MAR 29 | 2154 MAR 31 |
| 1655 APR 15 | 1755 MAR 30 | 1855 APR 8 | 1955 APR 10 | 2055 APR 18 | 2155 APR 20 |
| 1656 APR 6 | 1756 APR 18 | 1856 MAR 23 | 1956 APR 1 | 2056 APR 2 | 2156 APR 11 |
| 1657 MAR 29 | 1757 APR 10 | 1857 APR 12 | 1957 APR 21 | 2057 APR 22 | 2157 MAR 27 |
| 1658 APR 11 | 1758 MAR 26 | 1858 APR 4 | 1958 APR 6 | 2058 APR 14 | 2158 APR 16 |
| 1659 APR 3 | 1759 APR 15 | 1859 APR 24 | 1959 MAR 29 | 2059 MAR 30 | 2159 APR 8 |
| 1660 APR 22 | 1760 APR 6 | 1860 APR 8 | 1960 APR 17 | 2060 APR 18 | 2160 MAR 23 |
| 1661 APR 14 | 1761 MAR 22 | 1861 MAR 31 | 1961 APR 2 | 2061 APR 10 | 2161 APR 12 |
| 1662 MAR 30 | 1762 APR 11 | 1862 APR 20 | 1962 APR 22 | 2062 MAR 26 | 2162 APR 4 |
| 1663 APR 19 | 1763 APR 3 | 1863 APR 5 | 1963 APR 14 | 2063 APR 15 | 2163 APR 24 |
| 1664 APR 10 | 1764 APR 22 | 1864 MAR 27 | 1964 MAR 29 | 2064 APR 6 | 2164 APR 8 |
| 1665 MAR 26 | 1765 APR 7 | 1865 APR 16 | 1965 APR 18 | 2065 MAR 29 | 2165 MAR 31 |
| 1666 APR 15 | 1766 MAR 30 | 1866 APR 1 | 1966 APR 10 | 2066 APR 11 | 2166 APR 20 |
| 1667 APR 7 | 1767 APR 19 | 1867 APR 21 | 1967 MAR 26 | 2067 APR 3 | 2167 APR 5 |
| 1668 MAR 22 | 1768 APR 3 | 1868 APR 12 | 1968 APR 14 | 2068 APR 22 | 2168 MAR 27 |
| 1669 APR 11 | 1769 MAR 26 | 1869 MAR 28 | 1969 APR 6 | 2069 APR 14 | 2169 APR 16 |
| 1670 APR 3 | 1770 APR 15 | 1870 APR 17 | 1970 MAR 29 | 2070 MAR 30 | 2170 APR 1 |
| 1671 APR 23 | 1771 MAR 31 | 1871 APR 9 | 1971 APR 11 | 2071 APR 19 | 2171 APR 21 |
| 1672 APR 7 | 1772 APR 19 | 1872 MAR 31 | 1972 APR 2 | 2072 APR 10 | 2172 APR 12 |
| 1673 MAR 30 | 1773 APR 11 | 1873 APR 13 | 1973 APR 22 | 2073 MAR 26 | 2173 APR 4 |
| 1674 APR 19 | 1774 APR 3 | 1874 APR 5 | 1974 APR 14 | 2074 APR 15 | 2174 APR 17 |
| 1675 APR 4 | 1775 APR 16 | 1875 MAR 28 | 1975 MAR 30 | 2075 APR 7 | 2175 APR 9 |
| 1676 MAR 26 | 1776 APR 7 | 1876 APR 16 | 1976 APR 18 | 2076 APR 19 | 2176 MAR 31 |
| 1677 APR 15 | 1777 MAR 30 | 1877 APR 1 | 1977 APR 10 | 2077 APR 11 | 2177 APR 20 |
| 1678 MAR 31 | 1778 APR 19 | 1878 APR 21 | 1978 MAR 26 | 2078 APR 3 | 2178 APR 5 |
| 1679 APR 20 | 1779 APR 4 | 1879 APR 13 | 1979 APR 15 | 2079 APR 23 | 2179 MAR 28 |
| 1680 APR 11 | 1780 MAR 26 | 1880 MAR 28 | 1980 APR 6 | 2080 APR 7 | 2180 APR 16 |
| 1681 APR 3 | 1781 APR 15 | 1881 APR 17 | 1981 APR 19 | 2081 MAR 30 | 2181 APR 1 |
| 1682 APR 16 | 1782 MAR 31 | 1882 APR 9 | 1982 APR 11 | 2082 APR 19 | 2182 APR 21 |
| 1683 APR 8 | 1783 APR 20 | 1883 MAR 25 | 1983 APR 3 | 2083 APR 4 | 2183 APR 13 |
| 1684 MAR 30 | 1784 APR 11 | 1884 APR 13 | 1984 APR 22 | 2084 MAR 26 | 2184 MAR 28 |
| 1685 APR 19 | 1785 MAR 27 | 1885 APR 5 | 1985 APR 7 | 2085 APR 15 | 2185 APR 17 |
| 1686 APR 4 | 1786 APR 16 | 1886 APR 25 | 1986 MAR 30 | 2086 MAR 31 | 2186 APR 9 |
| 1687 MAR 27 | 1787 APR 8 | 1887 APR 10 | 1987 APR 19 | 2087 APR 20 | 2187 MAR 25 |
| 1688 APR 15 | 1788 MAR 23 | 1888 APR 1 | 1988 APR 3 | 2088 APR 11 | 2188 APR 13 |
| 1689 MAR 31 | 1789 APR 12 | 1889 APR 21 | 1989 MAR 26 | 2089 APR 3 | 2189 APR 5 |
| 1690 APR 20 | 1790 APR 4 | 1890 APR 6 | 1990 APR 15 | 2090 APR 16 | 2190 APR 25 |
| 1691 APR 12 | 1791 APR 24 | 1891 MAR 29 | 1991 MAR 31 | 2091 APR 8 | 2191 APR 10 |
| 1692 MAR 27 | 1792 APR 8 | 1892 APR 17 | 1992 APR 19 | 2092 MAR 30 | 2192 APR 1 |
| 1693 APR 16 | 1793 MAR 31 | 1893 APR 2 | 1993 APR 11 | 2093 APR 12 | 2193 APR 21 |
| 1694 APR 8 | 1794 APR 20 | 1894 MAR 25 | 1994 APR 3 | 2094 APR 4 | 2194 APR 6 |
| 1695 MAR 24 | 1795 APR 5 | 1895 APR 14 | 1995 APR 16 | 2095 APR 24 | 2195 MAR 29 |
| 1696 APR 12 | 1796 MAR 27 | 1896 APR 5 | 1996 APR 7 | 2096 APR 15 | 2196 APR 17 |
| 1697 APR 4 | 1797 APR 16 | 1897 APR 18 | 1997 MAR 30 | 2097 MAR 31 | 2197 APR 9 |
| 1698 APR 24 | 1798 APR 8 | 1898 APR 10 | 1998 APR 12 | 2098 APR 20 | 2198 MAR 25 |
| 1699 APR 9 | 1799 MAR 24 | 1899 APR 2 | 1999 APR 4 | 2099 APR 12 | 2199 APR 14 |
Sķšasta višbót 22.2. 2017