Í þessum kafla er ætlunin að taka til meðferðar reglu til að finna aldur tungls á hverjum tíma, hvenær það er nýtt og hvenær fullt. Um þessa reglu má segja, líkt og um aðrar reglur fingrarímsins, að hún getur verið hvort tveggja í senn, skemmtileg dægrastytting og hagnýt reikningslist. Meðal þeirra sem gætu haft not af slíkri rímreglu eru fræðimenn sem fást við tímasetningu atburða og tímatal.  Í gömlum heimildum er þess stundum getið hvernig staðið hafi á tungli þegar tiltekinn atburður gerðist. Þetta er skiljanlegt þegar það er haft í huga, að allt fram til þess tíma að raflýsing kom til sögunnar, fylgdist þorri manna náið með gangi tungls. Var þá til dæmis algengt að menn höguðu ferðum sínum eftir því hvort bjart var af tungli um nætur. Þótt tímarnir séu breyttir, getur tunglskin enn skipt nokkru máli, einkanlega í dreifbýli og þegar sérstaklega stendur á, t.d. við stjörnuskoðun. Þá er algengt að menn hugi að gangi tungls vegna áhrifa þess á sjávarföll. Ef almanak er ekki við höndina, og eins þegar horft er langt fram eða aftur í tímann, getur fingrarímið komið að góðum notum.
 

Lengd tunglmánaðarins

Meðallengd tunglmánaðar frá nýju tungli til nýs tungls er 29,53 dagar, nánar tiltekið 29,53059 dagar eða 29 dagar 12 stundir 44 mínútur og 3 sekúndur ef meðaltalið er tekið yfir langt tímabil (heila öld eða meira). Þetta meðaltal er býsna stöðugt frá einni öld til annarrar, og er það forsenda þess að unnt er að setja fram tiltölulega aðgengilegar rímreglur um gang tunglsins, á borð við þær sem notaðar eru við útreikning páskanna. En þótt meðallengd tunglmánaðarins breytist lítið, er gangur tungls samt háður verulegum sveiflum sem valda því að lengd einstakra tunglmánaða er talsvert breytileg, allt frá 29,28 dögum upp í 29,83 daga. Munur stysta og lengsta tunglmánaðar er því 0,55 dagar eða 13 stundir. Breytileikinn kemur einnig fram í því að fullt tungl er ekki alltaf í tunglmánuðinum miðjum. Tíminn sem líður frá því að tungl er nýtt þar til það er fullt, er því ekki alltaf jafnlangur tímanum sem líður frá því að það er fullt og þar til það er aftur nýtt. Getur munurinn numið 1,6 dögum.

Ég hef séð ástæðu til að tilgreina þessi frávik hér, þar sem erfitt er að hafa upp á þeim í stjörnufræðilegum heimildum, og  hef ég orðið að styðjast við eigin útreikninga til að finna hin tölulegu gildi.

Af ofangreindu er væntanlega ljóst, að til þess að ákvarða tunglkomur og tunglfyllingar með nákvæmni í fortíð og framtíð þarf umtalsverða stjarnfræðilega útreikninga. Fingrarímið getur auðvitað ekki komið í staðinn fyrir slíka útreikninga, en það hefur þann kost að vera fljótvirkt og gefur svör sem eru nægilega nákvæm til almennustu nota. Hve stórar skekkjurnar geta orðið er spurning sem rædd verður síðar í þessum kafla.
 

Aldur tungls, paktar og paktaleiðrétting

Aldur tungls er sá dagafjöldi sem liðinn er frá því að tungl var nýtt. Ef við þekkjum aldur tungls i upphafi árs, getum við sagt til um það nokkurn veginn hvenær í janúar sé von á nýju tungli. Jafnframt getum við áætlað hvenær tunglkomur verði seinna á árinu, ef við gerum ráð fyrir að tunglmánuðirnir fylgi meðallengd.

Hér kemur að góðu haldi hjálpartalan paktar sem notuð var við útreikning páskanna. Paktar tiltekins árs samsvara í vissum skilningi aldri tungls á nýársdag (sjá nánar í greininni um grundvöll páskareiknings í Almanaki Þjóðvinafélagsins 1971, bls. 163 og 160). Paktarnir geta tekið öll gildi frá 0 upp í 29. Paktatalan 30, sem stundum er notuð, jafngildir 0. Á bls. 2 í Almanaki Háskólans er ávallt sýnt hverjir eru paktar ársins.

Í kafla III var sýnt hvernig hægt væri að finna pakta tiltekins árs með fingrarími eða reiknireglum. Þær aðferðir verða ekki rifjaðar upp hér að öðru leyti en því, að gera þarf nokkurn fyrirvara um notkun þeirra við tunglreikninga í gamla stíl (júlíanska tímatalinu). Umræddar reglur voru nefnilega samdar með það fyrir augum að þær segðu til um fyllingardag páskatungls eins og hann er sýndur í þeim kirkjulegu tungltöflum sem páskarnir miðast við. Tungltöflur kirkjunnar eru í allgóðu samræmi við meðalgang tunglsins í nýja stíl, en í gamla stíl gætti verulegs misræmis, einkanlega undir lokin. Þess vegna er nauðsynlegt að endurskoða útreikning pakta í gamla stíl ef paktarnir eiga að sýna réttan aldur tungls fremur en aldur þess samkvæmt kirkjulegum tungltöflum. Endurskoðunin er í því fólgin að paktaleiðréttingin (sjá fyrr) er lagfærð í gamla stíl og verður þar breytileg, en var áður föst (+7).

Paktaleiðréttingin verður þá sem hér segir, frá árinu 0 (þ.e. 1 f. Kr.) til ársins 2199 e. Kr.

Tölurnar í svigum eru jafngildistölur þannig að einu gildir hvor talan er notuð. Taflan er miðuð við tímareikning á Íslandi, og tekur nýi stíll því við af gamla stíl í nóvember árið 1700. Frá 1. janúar til 16. nóvember það ár gildir paktaleiðréttingin +10, en frá 28. nóvember til ársloka er leiðréttingin –1 (sem jafngildir +29). Dagsetningarnar 17.- 27. nóvember féllu niður.

Paktaleiðréttingin breytist árin 300, 600, 900, 1200 og 1500 í gamla stíl, en árin 1700 og 1900 í nýja stíl. Til skýringar á þessu skal enn vísað í greinina um grundvöll páskareiknings í Almanaki Þjóðvinafélagsins 1971, bls. 168-169. Einföld minnisregla til að finna paktaleiðréttinguna í gamla stíl er sem hér segir: Athugið hve oft talan 300 gengur upp í ártalinu, sleppið afgangi en leggið 5 við útkomuna. Dæmi: 1377. Ef 300 er deilt í ártalið verður útkoman 4, og þegar 5 er bætt við, fæst paktaleiðréttingin 9.
 

Reikniregla til að finna pakta

Paktaleiðréttingin gengur á einfaldan hátt inn í paktareglu fingrarímsins, og þeir sem kunna þá reglu ættu nú að geta fundið þá pakta sem gilda fyrir tunglreikning jafnauðveldlega og hina sem gilda við útreikning páskanna.

Öðru máli gegnir ef menn ætla að nota reiknireglur til að finna paktana. Tvær slíkar reglur voru gefnar í kafla III, önnur fyrir nýja stíl en hin fyrir gamla stíl. Þessar reglur fólu í sér paktaleiðréttingu, en með óbeinum hætti, og er því ekki vandalaust fyrir hinn almenna lesanda að taka tillit til breyttrar paktaleiðréttingar. Til hægðarauka skal því sett hér fram sameiginleg regla fyrir paktareikning í gamla stíl og nýja stíl þar sem paktaleiðréttingin er notuð líkt og í fingraríminu. Reglan er þessi:

Takið ártalið og deilið í það með 19. Afganginn skal margfalda með 11, leggja 1 við og síðan paktaleiðréttinguna. Þegar deilt er í útkomuna með 30 verður afgangurinn paktarnir. Ef útkoman er neikvæð tala leggjast 30 við.

Dæmi: 1976. Við deilum í ártalið með 19, deilingin gengur upp svo að afgangur er 0. Núll margfaldað með 11 er aftur 0, síðan leggjum við 1 þar við og loks paktaleiðréttinguna sem er –2 (eða +28). Summan er –1 (eða 29). Deilum í hana með 30, og afgangurinn verður–1 (eða 29). Paktarnir eru því 29.

Aftast í þessum kafla eru töflur sem sýna pakta fyrir öll ár frá 0 til 2199 e. Kr.
 

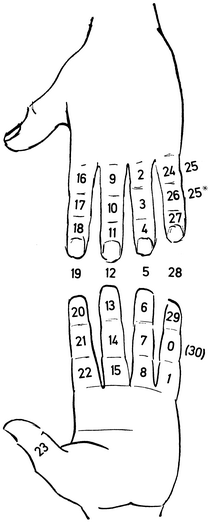
Notkun paktanna í fingraríminu

Hugsum okkur nú að paktatölunum frá 0 til 29 sé raðað niður á fingur vinstri handar eins og sýnt er á 28. mynd. Myndin er öldungis eins og 27. mynd þar sem verið var að sýna notkun pakta við páskareikning. Tölunum er raðað kerfisbundið á fingurna, byrjað með 0 á innanverðum miðlið litlafingurs og talið fram á 23 á upplið þumalfingurs. Þaðan er stokkið yfir á utanverðan upplið litlafingurs og hringnum lokað við 30 = 0. Tölurnar 5, 12, 19 og 28 lenda á fingurtoppunum. Talan 25 er ýmist sett á sama stað og talan 24 eða látin fylgja tölunni 26 og þá auðkennd með stjörnu (*). Hið síðara fyrirkomulag gildir m.a. á yfirstandandi öld eins og sjá má á paktatöflunum hér að neðan. Á tímabilinu 0-2199 koma paktarnir 25* í stað 25 þegar paktaleiðréttingin er 6, 9 eða –2.

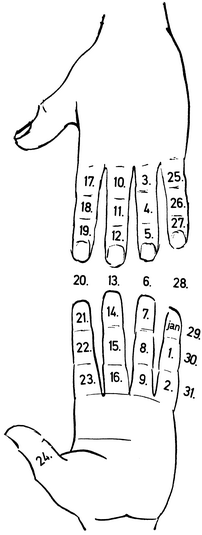
Við skulum nú taka árið 1976 sem dæmi og nota fingrarímið til að finna aldur tungls í janúarmánuði. Paktar ársins eru 29 eins og áður er sagt, og sú tala situr á framlið litlafingurs innanverðum. Þann stað köllum við aðfararstað ársins, og er hann jafnframt aðfararstaður janúarmánaðar. Frá aðfararstaðnum teljum við nú daga mánaðarins og færum okkur frá einum fingurstað yfir á þann næsta eftir sömu leið og mörkuð var með paktatölunum (sjá 29. mynd). 1. janúar lendir á miðlið litlafingurs innanverðum, 2. janúar á uppliðnum innanverðum, 3. janúar á upplið baugfingurs utanverðum, 4. janúar á miðlið baugfingurs utanverðum, og svo áfram hringinn. Hringurinn hefur aðeins 29 sæti svo að 30. janúar lendir á sama stað og 1. janúar, og 31. janúar lendir á sama stað og 2. janúar.

Ef við heimfærum nú 29. mynd upp á 28. mynd sjáum við að 1. janúar stendur á sama fingurstað og paktatalan 0, 2. janúar á sama stað og paktatalan 1, 3. janúar á sama stað og paktatalan 2, og svo framvegis. Þetta ber að túlka á þann hátt að 1. janúar sé aldur tungls 0 dagar, þ.e. að tungl sé nýtt þann dag, 2. janúar sé tungl eins dags gamalt, 3. janúar tveggja daga gamalt, o.s.frv. Ef við höldum áfram til 30. janúar erum við komin heilan hring og lendum þá í annað sinn á innanverðum miðlið litlafingurs þar sem paktatalan 0 er fyrir; þann dag ætti þá aftur að vera nýtt tungl samkvæmt reglunni. Dagsetningin 26. janúar fellur á fingurstað þar sem tvær paktatölur standa, 25* og 26, og telst aldur tungls þá vera 25-26 dagar, þar eð báðar tölurnar eru jafnlíklegar.

Aðferðin til þess að finna aldur tungls í öðrum mánuðum er hliðstæð aðferðinni fyrir janúarmánuð; hið eina sem breytist er aðfararstaðurinn. Aðfararstaðir mánaðanna fylgja hver öðrum á kerfisbundinn hátt þannig að við getum rakið okkur áfram frá aðfararstað janúar:   aðfararstaður febrúar er á næsta fingurstað, aðfararstaður marsmánaðar er hinn sami og janúarmánaðar, en síðan verður færsla um einn stað fyrir hvern mánuð sem á eftir fer, allt til ársloka eins og hér er sýnt:

                                                       janúar, mars
                                                       febrúar, apríl
                                                       maí
                                                       júní
                                                       júlí
                                                       ágúst
                                                       september
                                                       október
                                                       nóvember
                                                       desember

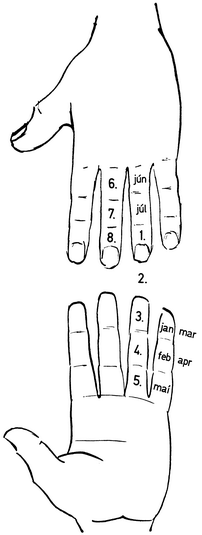
Þetta verður best skýrt með dæmi. Setjum svo að við viljum finna aldur tungls 8. júlí 1976 (sjá 30. mynd). Við byrjum eins og áður á aðfararstað ársins, á framlið litlafingurs innanverðum, og segjum þar "janúar", færum okkur næst á miðliðinn og segjum "febrúar", síðan til baka á framliðinn og segjum "mars", þá á miðliðinn og segjum "apríl", þaðan á uppliðinn og segjum "maí". Næsti staður er á upplið baugfingurs utanverðum, og þar segjum við "júní". Þegar komið er á miðlið baugfingurs utanverðan segjum við loks "júlí". Þar er þá aðfararstaður mánaðarins. Frá þeim stað teljum við svo dagana: 1. júlí lendir á framlið baugfingurs utanverðum, 2. júlí á fingurtoppinum, 3. júlí á framliðnum innanverðum, 4. júlí á miðliðnum innanverðum, 5. júlí á uppliðnum innanverðum, 6. júlí á upplið löngutangar utanverðum, 7. júlí á miðlið löngutangar utanverðum og 8. júlí á framlið löngutangar utanverðum. Þar stendur paktatalan 11, sem er þá aldur tungls hinn 8. júlí.

Tökum annað dæmi: Hvenær verður nýtt tungl í desember 1977? Paktar ársins eru 10 og sú tala situr á utanverðum miðlið löngutangar. Við segjum "janúar" þar, færum okkur á framliðinn og segjum "febrúar", aftur á miðliðinn og segjum "mars", síðan á framliðinn og segjum "apríl", þá á fingurtoppinn og segjum "maí", á framliðinn innanverðan og segjum "júní", miðliðinn innanverðan og segjum "júlí", uppliðinn innanverðan og segjum "ágúst"; þar næst flytjum við okkur yfir á utanverðan upplið vísifingurs og segjum "september", þaðan á miðlið vísifingurs utanverðan og segjum "október", á framliðinn utanverðan og segjum "nóvember" og loks á fingurtoppinn og segjum "desember". Við teljum nú áfram: 1. desember er á framlið vísifingurs innanverðum, 2. desember á miðliðnum innanverðum, 3. desember á uppliðnum innanverðum, 4. desember á upplið þumalfingurs, 5. desember á upplið litlafingurs utanverðum, 6. á miðlið litlafingurs utanverðum, 7. á framliðnum utanverðum, 8. á toppinum, 9. á framliðnum innanverðum og 10. á miðliðnum innanverðum. Þar stendur paktatalan 0 og er því nýtt tungl 10. desember.

Fullt tungl er að jafnaði 14-15 dögum á eftir nýju tungli (tímalengdin er breytileg, allt frá 13,9 dögum upp í 15,6 daga, en meðalgildið er 14,8 dagar) og finnst því á innanverðum miðlið eða upplið löngutangar. Með því að telja áfram í desember 1977 finnum við að fullt tungl er 24.-25. desember, og hefði því átt að vera tunglskin á jólanóttina það árið.

Þriðja og síðasta dæmið sem við skulum taka er að finna aldur tungls við Flugumýrarbrennu árið 1253. Almennt er talið að sá atburður hafi gerst aðfaranótt 22. október, og gæti verið fróðlegt að vita hvort bjart hafi verið af tungli þegar aðförin var gerð. Paktar ársins eru 28, og sú tala situr á toppi litlafingurs. Við byrjum að telja þar og segjum "janúar", rekjum okkur síðan áfram og finnum aðfararstað október sem reynist vera á toppi baugfingurs. 1. október lendir þá á innanverðum framlið baugfingurs, og þegar við teljum áfram daga mánaðarins á sama hátt og fyrr, kemur í ljós að 22. október er á toppi litlafingurs. Tungl hefur þá verið 28 daga gamalt þessa nótt og aðeins vantað tvo daga í nýtt tungl. Af því má ráða að nótt hafi verið dimm, niðamyrkur í orðsins fyllstu merkingu.

Fljótt á litið gæti mönnum virst að tíminn hafi þarna verið vel valinn til árásar. En þá kemur hitt til álita, hvort ekki hefðu verið talin tormerki á því að berjast í slíku myrkri með kyndla eina til lýsingar. Um slíkt má lengi deila, en spurningin gefur tilefni til að athuga dagsetningar nánar.

Dagsetningin 22. október er sótt í fornar ártíðaskrár, þar á meðal Helgafellsskrá (sjá Íslenskar ártíðaskrár eftir dr. Jón Þorkelsson, bls. 66, 87, 91 og 118). En þegar flett er upp í Sturlungu, kemur misræmi í ljós. Brúðkaup Halls og Ingibjargar "skyldi vera at vetrnóttum á Flugumýri". Frásögnin af brúðkaupinu hefst "föstukveld it síðasta í sumri" og er síðan rakin rás atburða allt fram á "þriðjakveldit" þegar atlagan var gerð. Með því að nota fingrarímið er fljótlegt að ganga úr skugga um, að vetrarkoma árið 1253 var 11. október. Næsti þriðjudagur á eftir er þá 14. október, og er það sú dagsetning brennunnar, sem ráða má af Sturlungu. (Í formála sem dr. Jón Jóhannesson ritar fyrir útgáfu Sturlungu árið 1946 (2. bindi, bls. LIII) kemur fram, að dr. Jóni er kunnugt um þetta misræmi í dagsetningum og telur það þurfa nánari rannsóknar við.) Sé þetta rétt, hefur tungl verið á þriðja kvartili og tunglskins að vænta, a.m.k. þegar líða tók á nóttina.  (Nákvæmir útreikningar sýna að tungl hefur verið fullt hinn 8. október og nýtt hinn 24. október árið 1253.) Frá sjónarmiði árásarmanna hefðu skilyrði þá mátt teljast fremur hagstæð. En hvort sem menn vilja trúa því að Flugumýrarbrenna hafi átt sér stað aðfaranótt 15. október, eða halda sér við hina hefðbundnu dagsetningu 22. október, er þetta frambærilegt dæmi um notagildi fingrarímsins.

Sú aðferð sem hér hefur verið lýst til að finna aldur tungls með fingrarími er jafnfljótvirk, hvort sem farið er lengra eða skemmra fram eða aftur í tímann. Í fingrarími Jóns biskups Árnasonar er gyllinital notað í stað pakta til að finna tunglkomur. Aðferð Jóns er í sjálfu sér ágæt, en gildi hennar takmarkast við tímabilið 1700-1899, og þótt unnt sé að laga hana að öðrum tímaskeiðum, er það ekki svo einfalt mál að hún verði með nokkru móti hentug sem almenn regla. Einnig má benda á, að sú fingrarímsregla sem hér hefur verið sett fram, hefur þann kost fram yfir aðferð Jóns að vera nátengd reglunni til að finna páska. Krefst hún því lítils viðbótarlærdóms.
 

Reikningsaðferð til að finna aldur tungls

Í viðauka við fingrarím Jóns biskups er sagt frá aðferð til að finna aldur tungls eftir pöktum. Þarna er um reikningsaðferð að ræða en ekki fingrarímsreglu, en aðferðin er svo einföld að mér finnst sjálfsagt að láta hana fylgja hér með. Aðferðin er þessi: Takið pakta ársins, leggið mánaðardaginn við og síðan viðbótartölu sem er 1 fyrir janúar (0 í hlaupári), 2 fyrir febrúar (1 í hlaupári), 1 fyrir mars, 2 fyrir apríl, 3 fyrir maí, 4 fyrir júní, 5 fyrir júlí, 6 fyrir ágúst, 7 fyrir september, 8 fyrir október, 9 fyrir nóvember og 10 fyrir desember (latnesku töluorðin septem, octo, novem og decem eiga þarna vel við). Útkoman gefur þá aldur tungls umræddan mánaðardag. Ef útkoman fer yfir 30 dragast 30 frá svo oft sem nauðsyn krefur til að fá lægri tölu en 30.

Sem dæmi skulum við finna aldur tungls á gamlársdag 1978. Paktar eru 21. Við leggjum dagsetninguna 31 við og fáum 52, bætum svo 10 við fyrir desember og útkoman verður 62. Þar frá dragast 30 tvisvar og eftir standa 2, sem er þá aldur tungls þennan dag.

Reikningsaðferð þessi er náskyld fingrarímsreglunni sem fyrr er lýst, en þó getur munað degi á niðurstöðunni. Sú er einmitt raunin í þessu síðasta dæmi eins og lesandinn getur sjálfur sannprófað. Í þetta skipti er það reikningsaðferðin sem gefur réttari niðurstöðu, en svo er ekki alltaf. Staðreyndin er sú, að engin einföld regla, hvorki reikniformúla né fingrarímsregla, nægir til að ákvarða aldur tungls með fullri nákvæmni í öllum tilvikum.

Nú er eðlilegt að lesandinn spyrji, hve oft megi vænta skekkju þegar fingrarímið er notað við tunglreikninga, og hve stór skekkjan geti orðið. Skal nú reynt að svara þeirri spurningu.
 

Frávik rímtungls frá réttu tungli

Þegar fingrarím er notað til að finna aldur tungls, geta ýmsir skekkjuvaldar haft áhrif á niðurstöðuna. Má þar nefna (a) sveiflur í gangi tungls sem geta valdið því að rétt tungl verði allt að 0,60 dögum (14 stundum) á undan eða eftir meðaltungli, (b) misgengi tunglmánaða og almanaksmánaða, sem ekki er unnt að taka fullt tillit til, (c) sú fjögurra ára tímasveifla sem hlaupárin valda, (d) það misgengi tungls og pakta sem leiðrétt er í lok hverrar tunglaldar með því að hækka pakta um 12 í stað 11 milli ára, (e) það misgengi tungls og pakta sem lagfært er á aldamótum með tungljöfnuði og sóljöfnuði (breyttri paktaleiðréttingu), (f) mismunandi staðartími, sem veldur því m.a. að tunglkoma leikur á tveimur dagsetningum eftir því hvaða stað er miðað við.

Ef allir þessir skekkjuvaldar legðust á eitt, gæti frávikið af þeim sökum numið þremur dögum. Slíkt er þó mjög fátítt. Athugun á tunglkomum á 20. öld sýnir að 55% af þeim dagsetningum sem fingrarímið gefur eru réttar, 43 % eru einum degi á undan eða eftir áætlun, en tæplega 2% eru skakkar um tvo daga. Þriggja daga skekkjur koma ekki fyrir.

Á 19. öld eru hlutföllin þannig að 50% af tunglkomum fingrarímsins reynast rétt dagsettar, 47 % eru einum degi of snemma eða of seint, en 3% eru tveimur dögum frá réttu lagi. Þriggja daga skekkjur finnast ekki heldur á þeirri öld.

Í framhaldi af þessari athugun, sem gerð var með tölvu, var kannað hve oft þriggja daga skekkjur kæmu fyrir. Könnunin náði til tímabilsins 0-2199 e.Kr. (Hér eins og annars staðar í þessum texta merkir 0 árið 1 f.Kr.) Í ljós kom að þriggja daga skekkjur verða aðeins 8 sinnum á tímabilinu: í september árið 548, í maí 873, í maí og september 892, í september 1177, í september og nóvember 1196 og í september 1424. Öll eru frávikin í sömu átt þannig að rétt tunglkoma er þremur dögum fyrr en fingrarímið segir til um. Er þá reiknað í miðtíma Greenwich, en samkvæmt þeim tímareikningi voru umræddar tunglkomur allar að kvöldi dags, á tímanum frá kl. 18 til kl. 24.

Þegar reikniformúlan sem fyrr var lýst er notuð í stað fingrarímsins koma fram jafnmargar þriggja daga skekkjur á sama tímabili, en minni skekkjum fækkar nokkuð. Formúlan gerir greinarmun á paktatölunum 24 og 25, en ekki á tölunum 25 og 25*. Nú er augljóst, að gera verður greinarmun á 25 og 25* í páskareikningum, en spyrja má hvort þetta skipti máli við almenna tunglreikninga. Til að fá úr þessu skorið hef ég kannað hvaða áhrif það myndi hafa á nákvæmni fingrarímsins að nota eingöngu paktatöluna 25 (sem jafngildir 24) eða eingöngu paktatöluna 25* (sem jafngildir 26) í stað þess að nota þessar tölur til skiptis eftir því sem við á. Niðurstaðan varð sú, að slík einföldun drægi verulega úr nákvæmni rímsins. Er þetta í nokkurri mótsögn við þá staðhæfingu sumra fræðimanna, að sérreglan um paktatöluna 25* sé eingöngu til þess ætluð að dreifa dagsetningum páskadaga en leiði ekki til meiri nákvæmni í tungltöflum.

Til hægðarauka fyrir lesendur er hér birt tafla sem sýnir hvenær nýtt tungl verður í hverjum mánuði eftir fingraríminu fyrir hvert gildi sem paktar ársins taka. Í greininni um grundvöll páskareiknings í Almanaki Þjóðvinafélagsins 1971 er líka tafla sem sýnir tunglkomur eftir pöktum (á bls. 164), en sú tafla er ekki með öllu sambærileg við þessa því að hún sýnir tunglkomur í eldri merkingu þess orðs, eins og þar er reyndar útskýrt í texta.
 

Taflan miðast við tímatal á Íslandi, þ.e. gamla stíl fram í nóvember árið 1700 en nýja stíl eftir það. Í efstu línunni, fyrir neðan 1700, gildir fyrri talan (20) aðeins fyrir þann hluta ársins 1700 sem tilheyrir gamla stíl, en síðari talan (9) gildir í nýja stíl og þar með fyrir önnur ár í sömu línu (1719, 1738, 1757, 1776 og 1795).